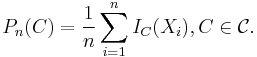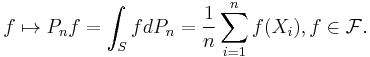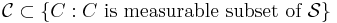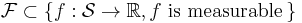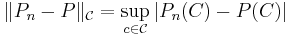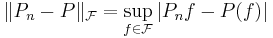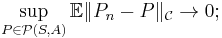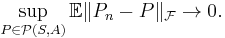Glivenko–Cantelli theorem
In the theory of probability, the Glivenko–Cantelli theorem, named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, determines the asymptotic behaviour of the empirical distribution function as the number of independent and identically distributed observations grows. This uniform convergence of more general empirical measures becomes an important property of the Glivenko–Cantelli classes of functions or sets.[1] The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning. Applications can be found in econometrics making use of M-estimators
Contents |
Glivenko–Cantelli theorem
Assume that 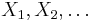 are independent and identically-distributed random variables in
are independent and identically-distributed random variables in  with common cumulative distribution function F(x). The empirical distribution function for
with common cumulative distribution function F(x). The empirical distribution function for  is defined by
is defined by
where 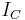 is the indicator function of the set
is the indicator function of the set  . For every (fixed) x,
. For every (fixed) x, 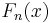 is a sequence of random variables which converge to F(x) almost surely by the strong law of large numbers, that is,
is a sequence of random variables which converge to F(x) almost surely by the strong law of large numbers, that is, 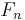 converges to F pointwise. Glivenko and Cantelli strengthened this result by proving uniform convergence of
converges to F pointwise. Glivenko and Cantelli strengthened this result by proving uniform convergence of 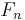 to F.
to F.
Theorem
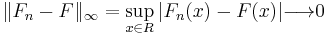 almost surely.[2]
almost surely.[2]
This theorem originates with Valery Glivenko,[3] and Francesco Cantelli,[4] in 1933.
Remarks
- If
 is a stationary ergodic sequence, then
is a stationary ergodic sequence, then  converges almost surely to
converges almost surely to 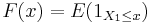 . The Glivenko–Cantelli theorem gives a stronger mode of convergence than this in the iid case.
. The Glivenko–Cantelli theorem gives a stronger mode of convergence than this in the iid case. - An even stronger uniform convergence result for the empirical distribution function is available in the form of an extended type of law of the iterated logarithm.[5] See asymptotic properties of the Empirical distribution function for this and related results.
Empirical measures
One can generalize the empirical distribution function by replacing the set ![(-\infty,x]](/2012-wikipedia_en_all_nopic_01_2012/I/b27ac59ac8e050f8343b712b19ae8f71.png) by an arbitrary set C from a class of sets
by an arbitrary set C from a class of sets  to obtain an empirical measure indexed by sets
to obtain an empirical measure indexed by sets 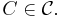
Further generalization is the map induced by 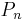 on measurable real-valued functions f, which is given by
on measurable real-valued functions f, which is given by
Then it becomes an important property of these classes that the strong law of large numbers holds uniformly on 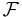 or
or  .
.
Glivenko–Cantelli class
Consider a set  with a sigma algebra of Borel subsets A and a probability measure P. For a class of subsets,
with a sigma algebra of Borel subsets A and a probability measure P. For a class of subsets,
and a class of functions
define random variables
where 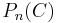 is the empirical measure,
is the empirical measure, 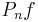 is the corresponding map, and
is the corresponding map, and
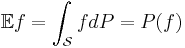 , assuming that it exists.
, assuming that it exists.
Definitions
- A class
 is called a Glivenko–Cantelli class (or GC class) with respect to a probability measure P if any of the following equivalent statements is true.
is called a Glivenko–Cantelli class (or GC class) with respect to a probability measure P if any of the following equivalent statements is true.
-
- 1.
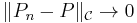 almost surely as
almost surely as 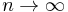 .
. - 2.
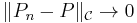 in probability as
in probability as 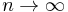 .
. - 3.
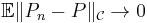 , as
, as 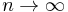 (convergence in mean).
(convergence in mean).
- 1.
- The Glivenko–Cantelli classes of functions are defined similarly.
- A class is called a universal Glivenko–Cantelli class if it is a GC class with respect to any probability measure P on (S,A).
- A class is called uniformly Glivenko–Cantelli if the convergence occurs uniformly over all probability measures P on (S,A):
Theorem (Vapnik and Chervonenkis,[6] 1968)
- A class of sets
 is uniformly GC if and only if it is a Vapnik–Chervonenkis class.
is uniformly GC if and only if it is a Vapnik–Chervonenkis class.
Examples
- Let
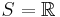 and
and ![{\mathcal C}=\{(-\infty,t]:t\in {\mathbb R}\}](/2012-wikipedia_en_all_nopic_01_2012/I/9ce3e42aef1b6790918794192f6f479f.png) . The classical Glivenko–Cantelli theorem implies that this class is a universal GC class. Furthermore, by Kolmogorov's theorem,
. The classical Glivenko–Cantelli theorem implies that this class is a universal GC class. Furthermore, by Kolmogorov's theorem,
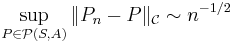 , that is
, that is  is uniformly Glivenko–Cantelli class.
is uniformly Glivenko–Cantelli class.
- Let P be a nonatomic probability measure on S and
 be a class of all finite subsets in S. Because
be a class of all finite subsets in S. Because  ,
, 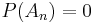 ,
, 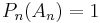 , we have that
, we have that 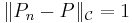 and so
and so  is not a GC class with respect to P.
is not a GC class with respect to P.
See also
- Donsker's theorem
- Dvoretzky–Kiefer–Wolfowitz inequality – strengthens Glivenko–Cantelli theorem by quantifying the rate of convergence.
Notes
- ^ van der Vaart, A.W. (1998) page 279
- ^ van der Vaart, A.W. (1998) page 265
- ^ Glivenko, V. (1933). Sulla determinazione empirica della legge di probabilita. Giorn. Ist. Ital. Attuari 4, 92-99.
- ^ Cantelli, F. P. (1933). Sulla determinazione empirica delle leggi di probabilita. Giorn. Ist. Ital. Attuari 4, 221-424.
- ^ van der Vaart, A.W. (1998) page 268
- ^ Vapnik, V.N. and Chervonenkis, A. Ya (1971). On uniform convergence of the frequencies of events to their probabilities. Theor. Prob. Appl. 16, 264-280
References
- van der Vaart, A.W. (1998) Asymptotic Statistics. Cambridge University Press. ISBN 0-521-78450-6
Further reading
-
- Dudley, R. M. (1999). Uniform Central Limit Theorems, Cambridge University Press. ISBN 0 521 46102 2.
- Shorack, G.R., Wellner J.A. (1986) Empirical Processes with Applications to Statistics, Wiley. ISBN 0-471-86725-X.
- van der Vaart, A.W. and Wellner, J.A. (1996) Weak Convergence and Empirical Processes, Springer. ISBN 0-387-94640-3.
![F_n(x)=\frac{1}{n}\sum_{i=1}^n I_{(-\infty,x]}(X_i),](/2012-wikipedia_en_all_nopic_01_2012/I/cd49533962f3a383ea2f7222791f6968.png)